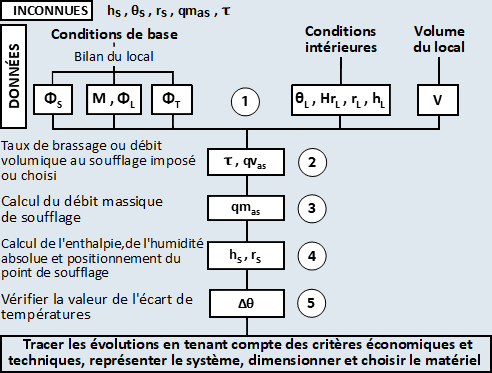
CONDITIONS DE SOUFFLAGE DANS UN LOCAL

Au préalable à l'étude des différents outils qui permettront de déterminer les conditions de soufflage (paramètres de l'air soufflé dans le local), il convient de rappeler que :

• les charges thermiques, hydriques et enthalpiques (somme algébrique des précédentes) sont connues et calculées à partir des caractéristiques du site et des caractéristiques géométriques de ce local (bilan thermique).
• les conditions intérieures sont connues et dépendent soit des critères de confort ou du processus industriel définis dans le cahier des charges.
• dans un système tout air, l'air soufflé est le vecteur utilisé pour maintenir l'équilibre thermohydrique du local étudié.

1. CONDITIONS DE BASE :

Déterminer les conditions de température et d'hygrométrie de l'environnement intérieur et extérieur constitue le point de départ d'un projet de climatisation ou de conditionnement d'air : ces conditions sont en général précisées dans le C.C.T.P (cahier des clauses techniques particulières du bâtiment ) et les documents ressources de la météorologie du site.

1.1) Conditions extérieures :

Elles dépendent de la saison et du lieu où est implanté le local à climatiser .
Les données météorologiques ont permis de fixer les températures sèches et les hygrométries.
Elles représentent la moyenne des valeurs maximales enregistrées.
Elles sont consignées dans des tableaux. Elles conduisent au calcul des charges maximales.
Pour la France, ces conditions sont répertoriées en fonction du département.

1.2) Conditions intérieures :

La température sèche et l'hygrométrie du local dépendent de son utilisation :

• Climatisation de confort (habitation, bureaux,grands magasins ...) : température et hygrométrie différentes pour chaque saison.
• Climatisation industrielle ou conditionnement d'air ( laboratoires, usines ... ) : température et hygrométrie dépendent du processus industriel. Elles peuvent être constantes toute l'année.

2. SYSTÈMES DE CLIMATISATION OU DE CONDITIONNEMENT D'AIR :

Ces systèmes de traitement d'air doivent contrer les charges thermiques et hydriques d'un local :

• Charges thermiques : Apports ou déperditions de chaleur externes et internes en [kW]
• Charges hydriques : Apports internes d'humidité en [kW] ou kg _eau /h].

En plus des charges thermiques et hydriques, le système doit assurer la qualité de l'air :

• le renouvellement d'air neuf hygiénique (maintien de la teneur en CO₂ et des odeurs à un niveau acceptable défini par la législation )
• la filtration de l'air soufflé ( contrôle de la teneur en poussières suivant la classe d'empoussièrement)

2.1) Différents systèmes :

Il existe plusieurs types de système que l'on peut classer en trois catégories :

Les systèmes tout air :

• centralisés (caisson unique pour l'ensemble des locaux)
• décentralisés (un système par local )
• multi-zone ( une C.T.A.N pour l'ensemble des traitements secondaires et différents pour les locaux ou groupe de locaux)

Les systèmes double conduits (ou gaines ) (air chaud / air froid) avec boîtes de mélange

Les systèmes eau/air : ventilo-convecteur ou pompe à chaleur réversible dans chaque local

2.2) Renouvellement d'air neuf : (air hygiénique) : (voir la page traitant ce sujet)

Plusieurs solutions technologiques existent pour l'apport d'air neuf hygiénique au local :

• Premier cas : L'air neuf, aux conditions extérieures, est mélangé à l'air recyclé par l'intermédiaire d'un caisson de mélange.
• Deuxième cas : L'air neuf est préparé dans une centrale dédiée (CTAN). ( Il est filtré, soit soufflé aux conditions de température et d'hygrométrie dans le local, soit soufflé aux conditions extérieures.

Lors de l'élaboration d'un projet, il faut connaître les caractéristiques de l'air neuf : c'est une donnée importante.
Si on n'en tient pas compte, le projet sera faussé, les éléments seront sous ou sur-dimensionnés suivant le cas.

2.3) Système tout air avec caisson de mélange :

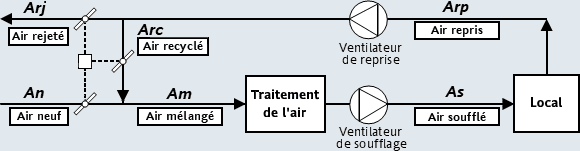
• Si le local est à la pression atmosphérique, on a : qm_An = qm_Arj et qm_As = qm_Arp

• Pour éviter les entrées d'air extérieur, la pression intérieure doit être légèrement supérieure à la pression atmosphérique: Ce procédé est souvent appliqué dans les salles propres (laboratoires, locaux aseptiques ... ).
  L'air extérieur ne peut s'infiltrer dans le local :
  • Pas de pollution par l'air extérieur puisqu'il ne peut y entrer (local équipé de portes étanches,sas )
  • Les fuites d'air sont préférables aux infiltrations d'air extérieur (énergie, confort ).

Dans ce cas, on a : qm_As > qm_Arp (débit As supérieur à débit Arp de 3 à 10 %)

• Le système devra combattre les charges du local et celles de l'air neuf.

• Le recyclage d'une partie de l'air du local permet d'effectuer une importante économie d'énergie c'est pourquoi on appelle le caisson de mélange un "économiseur".

• En hiver, il peut être intéressant d'admettre dans le local de l'air neuf à une enthalpie plus faible pour combattre gratuitement les charges thermiques et/ou hydriques du local : c'est le "Freecooling".

2.4 ) Système tout air en recyclage total :

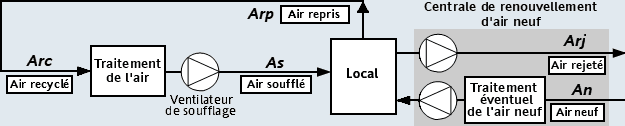
• Le système de traitement d'air principal n'apporte pas d'air neuf et ne rejette pas d'air vicié et on a : qm_An = qm_Arj = 0 et qm_As= qm_Arc = qm_Arp ( pour le système principal en recyclage total)
  
  
• Ce procédé impose que :
  • Soit le renouvellement d'air neuf est obtenu par un système de ventilation mécanique contrôlée. Le mélange d'air s'effectue directement dans le local. Le système devra combattre les charges du local et de l'air neuf apporté par la ventilation
  • Soit l'air neuf est préparé dans une centrale dédiée : L'air neuf est soufflé aux conditions intérieures du local.
    Un circuit d'air neuf particulier assure le renouvellement d'air neuf ( qm_Arj = qm_An).
    Le système ne doit combattre que les charges du local.

2.5 ) Système tout air air neuf :

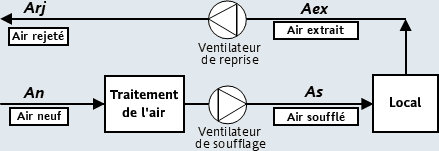
• Le débit de recyclage est nul : qm_arc= 0
• Si le local est à la pression atmosphérique : qm_as = qm_aex En surpression, on a : qmas > qm_aex
  
• Le système doit combattre les charges du local et surtout celles relatives à l'air neuf.
  
• Ce procédé n'est pas économique : c'est celui conduit aux puissances thermiques les plus élevées.
  Mais alors pourquoi l'utiliser ?
  Dans les salles propres (laboratoires d'analyse, blocs opératoires ), il n'est pas toujours possible de recycler l'air vicié du fait de sa contamination par les germes intrinsèques.
  Ainsi, pour diminuer les coûts énergétiques, on peut installer un récupérateur de chaleur :

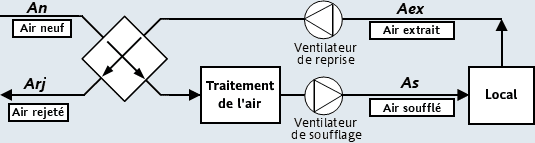
La puissance récupérable sur l'air extrait ( chaud ou froid) est transférée sur l'air neuf qui est soit réchauffé ou refroidi suivant la saison. Le temps de retour sur investissement est court. Ce procédé est le plus efficace lorsque les écarts de température (air neuf, air extrait ou air du local ) sont maximaux.

3. CHARGES D'UN LOCAL :

3.1 ) Charges sensibles :

Elles représentent la quantité de chaleur sous forme sensible apportée ou perdue par le local.
Elle est notée Φs et exprimée en kW.

3.1.1 ) Charges sensibles externes :

• Apports (été): essentiellement par ensoleillement et par conduction, convection, rayonnement
• Déperditions (hiver): par conduction, convection, infiltration d'air extérieur

Le signe de Φs dépend du type de charge : + pour des apports ou – pour des déperditions.

3.1.2 ) Charges sensibles internes:

Ce sont les apports de chaleur sous forme sensible pouvant provenir de machines électriques, de l'éclairage, des tuyauteries et conduits (souvent négligé), des occupants, des processus industriels.

3.2 ) Charges hydriques ou latentes :

Ce sont les apports de chaleur sous forme latente (dégagement d'humidité sous forme de vapeur d'eau ).
Ces dégagements d'humidité sont dus aux occupants, au processus industriel, au type de local (à fort dégagement d'humidité: piscine par exemple ).

Ces apports peuvent être exprimés de deux façons :

• Masse d'eau ou d'humidité : M en [kg_eau/h]
• Puissance : Φ _L en [kW]

Il existe une relation liant M et Φ_L : Φ_L= M . Lv avec Lv en [kJ/kg_eau], M en [kg/s] , Φ_L en [kW]

Lv est la chaleur latente de vaporisation de l'eau à la température intérieure du local. On la prend souvent égale à 2500 kJ/kg.

Si on veut plus de précision, il faudra lire cette valeur dans une table de vapeur d'eau ou la calculer à l'aide de la formule de Régnault : Lv = 2500,64 – 2,35.θ en [kJ/kg_eau]

3.3 ) Charges totales ou enthalpiques :

C'est la somme algébrique des charges sensibles et des charges latentes : Φ_T = Φ_S + Φ_L

Une attention particulière doit être apportée au calcul de Φ_T :

• Φ_S peut être négatif ou positif ( déperdition ou apport de chaleur )
• Φ_L est souvent positif ( apport d'humidité )

Dans certains cas, on peut avoir  | Φ_T | < | Φ_S | (en hiver, par exemple)  ( | | valeur absolue)

3.4 ) Expression des charges d'un local :

Les données peuvent être exprimées de plusieurs façons :

a) Φ_S et Φ_Len [kW] : on peut calculer directement Φ_T

b) Φ_T en [kW] et M en [kg_eau/h] : on calcule Φ_L puis Φ_S

c) Φ_S en [kW] et M en [kg_eau/h] : on calcule Φ_L puis Φ_T

4. BILAN ÉNERGÉTIQUE D'UN LOCAL :

Faire le bilan énergétique d'un local dont la température sèche et l'hygrométrie sont constantes (local en équilibre), c'est écrire :

• d'une part, que la puissance apportée au local ( par l'air soufflé,et les apports intérieurs) est égale à la puissance perdue par ce local (air extrait, repris ou perdu).
• d'autre part, que l'humidité apportée au local par l'air soufflé et les apports intérieurs d'humidité est égale à l'humidité perdue sous forme de condensation ou d'extraction d'air humide.

4.1 ) Bilan enthalpique ( chaleur totale : sensible + latent ) :

On prend comme hypothèse que :

• le débit massique d'air sec soufflé est égal au débit massique d'air repris ou extrait.
• les puissances et les masses d'eau apportées au local seront par convention affectées du signe +
• les puissances et les masses d'eau extraites du local seront par convention affectées du signe –

Le bilan enthalpique du local s'écrit : Φ₁ + Φ_T – Φ₂ = 0 ou Φ₁ + Φ_T = Φ₂

La puissance apportée au local par l'air soufflé s'écrit : Φ₁ = qm_as . h₁
La puissance apportée au local par les charges enthalpiques est : Φ_T
La puissance extraite du local par l'air repris ou extrait s'écrit : Φ₂ = qm_as . h₂

A partir des deux équations précédentes, on peut écrire :qm_as = Φ_T / ( h₂ – h₁)

Cette première relation amène des remarques importantes ; le débit massique d'air sec est toujours positif (ou non signé), de sorte que :

1) Si Φ_T > 0 , on a obligatoirement h₂ > h₁ ; ce qui signifie que l'air doit être soufflé à une enthalpie inférieure à celle de l'ambiance ( conditions de soufflage d'ÉTÉ en général)

2) Si Φ_T < 0 , on a obligatoirement h₂< h₁ ; ce qui signifie que l'air doit être soufflé à une enthalpie supérieure à celle de l'ambiance ( conditions de soufflage d'HIVER en général)

3) On connaît h₂ qui est l'enthalpie de l'air extrait ( l'air extrait peut être considéré comme représentatif de l'air ambiant si la distribution d'air est correcte et homogène). Attention ! ce n'est pas vrai pour tous les projets.

4) Pour calculer qm_as , il suffit de fixer h₁ c'est à dire les conditions de soufflage.

En d'autres mots, la puissance amenée par l'air au soufflage doit être de signe opposé à celle qui est apportée par le local.

4.2 ) Bilan sensible ( chaleur sensible seule) :

De la même manière, on peut écrire que : Φ_S1 + Φ_S - Φ_S2 = 0 Ou Φ_S1 + Φ_S = Φ_S2

La puissance apportée au local par l'air soufflé s'écrit : Φ_S1= qm_as . Cp₁ . θ₁
La puissance apportée au local par les charges sensibles est : Φ_S
La puissance extraite du local par l'air repris ou extrait s 'écrit : Φ_S2= qm_as . Cp₂ . θ₂

Cp₁ et Cp₂ représentent les capacités thermiques massiques respectives des deux airs soufflé et extrait.

Si nous ne tenons pas compte de la chaleur sensible de la vapeur d'eau dans l'air et en acceptant une approximation : qm_as ≈ Φ_S / [ Cp. ( θ₂ – θ₁ ) ]

Cette relation permettra de calculer rapidement le débit en avant-projet mais elle n'est pas rigoureuse même si l'erreur est très faible.
θ₂ – θ₁ représente l'écart de température appelé écart de soufflage en °C ou en K (Kelvin).

=> Ne pas l'utiliser lorsque le débit de soufflage est imposé et doit être calculé de façon très précise (salle propre par exemple).

4.3 ) Bilan d'humidité :

Pour l'humidité, on a : M₁ + M – M₂ = 0 Ou M₁ + M = M₂

La masse d'eau apportée au local par l'air soufflé s'écrit : M₁ =qm_as . r₁
La masse d'eau apportée au local par les charges hydriques est : M
La masse d'eau extraite du local par l'air repris ou extrait s'écrit : M₂ =qm_as . r₂

Donc, on a : qm_as = M / ( r₂ – r₁ ) et à partir de l'équation en 3.2), on peut aussi écrire que :  qm_as =  Φ_L / [ Lv . ( r₂ – r₁ ) ]

4.4 ) Rapport caractéristique j ou γ (gamma) :

Les relations en 4.1 et 4.3 permettent d'écrire : qm_as = Φ_T / ( h₂ – h₁) = M / ( r₂ – r₁ )

Donc : γ = Φ_T / M = ( h₂ – h₁) / ( r₂ – r₁ )  en [ kJ/ kg_eau ]
Ce rapport Φ_T / M est appelé rapport caractéristique du local.

Il représente la pente de la droite de charge du local appelée aussi droite de soufflage.

Les équations précédentes permettront de déterminer les coordonnées du point de soufflage sur le diagramme psychrométrique.

5. DÉTERMINATION DES CONDITIONS DE SOUFFLAGE :

Déterminer les conditions de soufflage de l'air dans le local c'est déterminer :

• Le débit massique d'air sec au soufflage qm_as en [kgas /s]
• Le taux de brassage 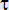en h^-1
• L'écart de température Δθ entre le soufflage et le local
• Les coordonnées du point de soufflage : deux paramètres suffisent à positionner le point sur le diagramme ( enthalpie h_s, température sèche θs , humidité absolue rs ... ).

Les conditions de soufflage permettront de dimensionner les éléments de l'installation : débit massique d'air, puissances, débits d'eau, de vapeur...

Pour le calcul, on fixe soit des valeurs :

• d'écart de températures au soufflage Δθ (dépendant directement de la technologie de diffusion de l'air)
• de taux de brassage 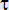(dépendant aussi du type de local et de la diffusion d'air)
• ou de débit volumique qv

Dans tous les cas, l'humidité relative du point de soufflage ne doit pas dépasser 90 % pour éviter la condensation de la vapeur d'eau dans le réseau de distribution d'air (soufflage).

5.1) Position du point de soufflage par rapport à celui du local :

La position du point de soufflage par rapport au point du local dépend du signe des charges sensibles et latentes.

Pour le local, on a : θ_L , r_L Pour le soufflage, on a : θ_S , r_S

Les charges sensibles peuvent être nulles ( = 0) , négatives (< 0) ou positives ( > 0).
Les charges latentes peuvent être de la même manière nulles ( = 0) , négatives (< 0) ou positives ( > 0).

Suivant les valeurs des charges, on peut considérer 9 positions significatives du point de soufflage par rapport au point du local :

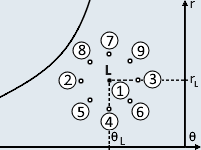
Connaissant le bilan thermique du local, on peut donc prévoir la position du point de soufflage.
Les positions 7,8,9 (au dessus de 2 et 3) sont rares car elles correspondent à des charges hydriques négatives.
Les positions 2 et 3 correspondent à des charges hydriques nulles.

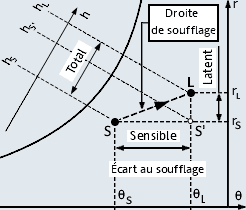
Étudions l'exemple du point 5 : Φ_S> 0 donc θ_S< θ_L  et Φ_L> 0 donc r_S < r_L

On peut écrire :

Bilan sensible : Φ_S = qm_as . ( h_S' - h_S ) ≈ qm_as . Cp. ( θ_L – θ_S )

Bilan latent : Φ_L = qm_as . ( h_L - h_S' ) = qm_as . Lv . ( r_L – r_S ) = M . Lv

Bilan total ou enthlapique : Φ_T = qm_as . ( h_L - h_S )

5.2) Caractéristique de l'écart de températures au soufflage :

L'écart de températures au soufflage représente la différence algébrique entre la température de soufflage et la température de l'ambiance (du local) : Δθ = θ_L– θ_S en [K] ou [°C]

Cet écart de températures :

• peut être positif ( l'air au soufflage est plus froid que l'air du local)
• peut être négatif ( l'air au soufflage est plus chaud que l'air du local )
• dépend de la capacité des dispositifs de diffusion à diffuser l'air sans gêne pour les occupants et de leur position dans le local.

On peut, en première approximation, prendre comme valeurs :

Soufflage froid  : Δθ de + 5 à + 12 K ( valeur courante + 10 K )
Soufflage chaud : Δθ de – 5 à – 20 K ( valeur courante – 20 K )

Le signe de cet écart n'est souvent pas renseigné ou donné en valeur absolue. Il faudra donc être attentif lors des calculs et du positionnement du point de soufflage sur le diagramme.

5.3) Définition du taux de brassage :

Le taux de brassage représente le nombre de volume d'air traité renouvelé dans le local pendant une heure :

= qv / V ou  qv = . V
avec :   taux de brassage en [vol.h^-1 ]
   V : Volume du local en [ m³]
   qv : débit volumique de soufflage en [m³/h]

Ce taux dépend évidemment du type de bouche de soufflage utilisé comme pour l'écart de soufflage puisqu'il exprime indirectement l'écart de soufflage.

Il ne dépasse pas 15 en climatisation de confort, peut aller jusqu'à 30 en conditionnement d'air et atteindre des valeurs très grandes ( 600) dans le cas de traitement d'air de salles blanches avec plafond diffusant.
La valeur courante en confort est de 7 à 8 environ.

5.4) Méthodes de détermination des conditions de soufflage :

Il existe plusieurs méthodes de détermination des conditions de soufflage.
Les méthodes traitées ne sont pas exhaustives : deux méthodes par calcul (exact ou approché) et trois méthodes graphiques.

5.4.1 Méthodes de détermination par calcul :

5.4.1.1 Premier cas : Température ou écart de températures au soufflage imposé

Remarque :

Si le système étudié est multi-saison (été, hiver), le calcul du débit massique conduit à deux résultats différents puisque les écarts de températures et les charges sont différents.

Pour le dimensionnement, il faut choisir le débit massique qui conduit aux conditions les plus défavorables, c'est à dire celles qui conduisent au débit massique le plus grand.

Le débit massique étant choisi, il faut recalculer l'écart de soufflage pour l'autre saison puisque le débit volumique reste constant quelque soit la saison (systèmes à débit constant). (Ce point sera développé dans un autre chapitre).

Relations caractéristiques :

Étape 1 : Données

Φ_T = Φ_S + Φ_L ; Φ_L = M . Lv ; Φ_S = Φ_T – Φ_L
Attention ! Φ_S , Φ_T peuvent être négatifs

Étape 2 : Calcul du débit massique

• Calcul rapide mais non rigoureux (précision suffisante pour un avant projet) :

En supposant que la capacité thermique massique de l'air reste constante, on peut, avec une bonne approximation, écrire : Φ_S = qm_as . Cp . ( θ_L– θ_S )

On déduit : qm_as ≈ Φ_S / [ Cp. ( θ_L– θ_S ) ] = Φ_S / ( θ_L– θ_S ) avec Cp = 1 kJ/kgas.K

• Calcul rigoureux mais plus long :

Il faut reprendre les équations qui incluent le débit massique et résoudre un système de quatre équations à quatre inconnues; ce qui permettra d'éliminer l'influence de Cp :

1 : Φ_T= qm_as. ( h_L – h_S)

2 : M = qm_as. ( r_L – r_S )

3 : h_L = θ_L + r_L . ( 2490 + 1,96 . θ_L )

4 : h_S = θ_S + r_S . ( 2490 + 1,96 . θ_S )

Attention : en fonction du diagramme utilisé comme support pour les tracés, il faudra prendre les coefficients respectifs de l'échelle des enthalpies ( coefficients 1.0000 / 2490 / 1.96 ; voir la définition de l'enthalpie massique )

La résolution mathématique conduit à l'expression :
qm_as = [ Φ_T – ( 2490 + 1,96 . θ_S ) . M ] / [ ( θ_L– θ_S ) . ( 1 + 1,96 . r_L ) ]

Étape 3 : Calcul de l'humidité absolue r_S :  M = qm_as . ( r _L – r_S )

Étape 6 : Calcul du taux de brassage et du débit volumique au soufflage : qv = qm_as .v"_s et = qv / V
puis on vérifie que la valeur du taux de brassage est correcte.

• Calcul de l'humidité absolue au soufflage (précis mais long) sans calcul préalable du débit massique :

La température de soufflage ou l'écart de soufflage est connu ou imposé.
Nous n'utilisons plus l'équation Φ_S = qm_as . Cp . ( θ_L– θ_S ) qui conduit à un résultat approché.

Il faut reprendre les équations et résoudre un système de quatre équations à quatre inconnues; ce qui permettra d'éliminer l'influence de Cp :

1 : Φ_T= qm_as. ( h_L – h_S)

2 : M = qm_as. ( r_L– r_S )

3 : h_L = θ_L + r_L . ( 2490 + 1,96 . θ_L )

4 : h_S = θ_S + r_S . ( 2490 + 1,96 . θ_S )

5 : γ = Φ_T / M

Les cinq équations précédentes permettent d'écrire : r_S = ( γ.r_L - h_L + θ_S ) / ( γ – 2490 – 1.96.θ_S )

5.4.1.2 Deuxième cas : Débit volumique au soufflage ou taux de brassage imposé

Étape 1 : Données

Φ_T = Φ_S + Φ_L ; Φ_L = M . Lv ; Φ_S = Φ_T – Φ_L Attention ! Φ_S , Φ_T peuvent être négatifs

Étape 2 : Calcul du débit volumique au soufflage : qv = . V ou qvas donné, imposé

Étape 3 : Calcul du débit massique au soufflage : qm_as = qv / v"_S

La difficulté du calcul du débit massique provient du fait que le volume spécifique de l'air au soufflage est une inconnue . Ce volume spécifique ne peut pas être lu ou calculé directement puisque l'on ne connaît pas les coordonnées du point de soufflage .

• Calcul rapide mais approximatif :

Pour lever l'indétermination, on se fixe arbitrairement un volume spécifique correspondant à une masse volumique spécifique de 1,2 kg/m³ ou un volume massique de 0,833 kg/m³. Dans ce cas, le calcul est très simple puisque le débit massique est égal à : qm_as= qv / v"_S = qv . ρ_S

Nota : Ce calcul simplifié n'est valable que si le bureau d'études ou le client n'impose pas expressément le débit volumique de soufflage ou le taux de brassage. Dans le cas d'applications de salles à atmosphère contrôlée (salles propres, laboratoires, ... ) , le cahier des charges ne permet pas d'utiliser cette méthode simplifiée.

• Calcul plus précis par itération :

L'équation à résoudre est : Φ_T = ( h_L – h_S ) . qv / v"_S ou Φ_T / qv = ( h_L - h_S ) / v"_S

Φ_T / qv est une constante pour le cas étudié.

Φ_T ,h_S, r_L , M, qv sont des données ; v"_S , h_S , θ_S , r_S sont inconnues.

1. En première itération, on calcule le débit massique en se fixant arbitrairement un volume spécifique égal au volume spécifique du local.
2. On calcule ensuite l'enthalpie : h_S = h_L – Φ_T / qm_as puis l'humidité : r_S = r_L – M / qm_as
3. On place provisoirement le point de soufflage obtenu. On lit h_S et v"_Ssur le diagramme ou on les calcule à partir de leur expressions respectives.
4. On calcule le nouveau débit massique et on recommence en (2.) trois ou quatre fois pour obtenir une précision suffisante ( 0,001 kg_as/s) , on trace la droite de soufflage.

Avec un peu de pratique, on réussit très vite en trois itérations.

Pour faciliter le calcul, on peut établir le tableau :

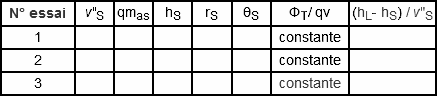
N° essai	v"S	qmas	hS	rS	θS	ΦT/ qv	(hL- hS) / v"S
1						constante
2						constante
3						constante

5.4.2 Méthodes de détermination par graphique :

Ces méthodes de détermination graphique sont très rapides, mais manquent de précision.
Il existe trois méthodes voisines dans le principe l'une de l'autre.

5.4.2.1 Méthode de "PORCHER" :

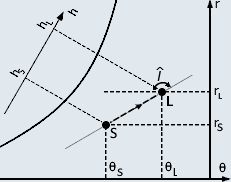
Cette méthode est basée sur le rapport caractéristique appelé ici j (équivalent à γ) par l'auteur de la méthode : j = Φ_T / M

• Ce rapport caractéristique est connu car le bilan thermique du local a été établi.
  Il représente la pente de la droite de charge du local ou droite de soufflage.
• Pour tracer la droite de soufflage, l'auteur de la méthode introduit la notion d'angle d'évolution î : angle formé par un isohydre(horizontale) et la droite de soufflage.

Construction de la droite de soufflage :

• Sur l'échelle fournie, on lit l'angle î correspondant à j.
• Issue du point L, on trace la droite inclinée de l'angle î par rapport à l'horizontale: c'est la droite de soufflage.
• Si l'écart de température est fixé, on connaît la température de soufflage.
• Le point de soufflage se trouve à l'intersection de cette droite de soufflage et de l'isotherme θ_S.

Cette méthode rapide souffre de l'imprécision dans la lecture de l'angle î correspondant au rapport caractéristique j.

6.4.2.2 Méthode de L' "A.I.C.V.F" :

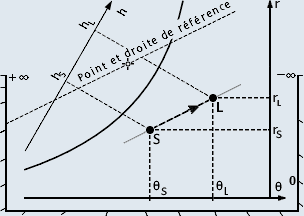
Elle est basée sur le même principe que la précédente puisqu'elle se base sur le rapport caractéristique : γ = Φ_T / M

La différence réside dans le report de cette pente pour le tracé de la droite de soufflage.
Ce report est presque direct puisque l'auteur de la méthode fourni sur son diagramme :

• Une échelle du rapport caractéristique variant de - infini à + infini
• Un point de référence pour le tracé de la parallèle à la droite de soufflage cherchée.

Construction de la droite de soufflage :

• Sur l'échelle fournie, on lit directement la valeur du rapport γ
• On trace une droite issue du point de référence jusqu'à la valeur du rapport γ
• On trace une parallèle à cette droite de référence passant par le point du local L
• Le point de soufflage se trouve à l'intersection de cette droite de soufflage et l'isotherme θ_S

Cette méthode rapide est un peu plus précise que la précédente.

6.4.2.3 Méthode de "CARRIER" :

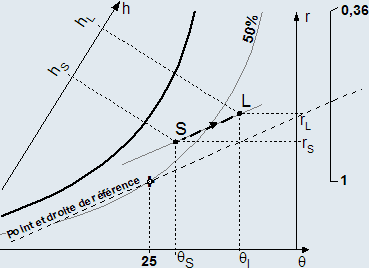
Elle est basée sur le facteur de chaleur sensible : SHF = Φ_S / Φ_T

Ce report est presque direct puisque l'auteur de la méthode fourni sur son diagramme :

• Une échelle du facteur de chaleur sensible variant de 0,36 à 1
• Un point de référence pour le tracé de la parallèle à la droite de soufflage cherchée.

Construction de la droite de soufflage :

• Sur l'échelle fournie, on lit directement la valeur du facteur de chaleur sensible S.H.F
• On trace une droite issue du point de référence (25°C,50 %) jusqu'à la valeur du S.H.F
• On trace une parallèle à cette droite de référence passant par le point du local L
• Le point de soufflage se trouve à l'intersection de cette droite de soufflage et l'isotherme θ_S

Cette méthode simple et rapide présente l'inconvénient de ne pas être utilisable pour les charges sensibles négatives c'est à dire les charges d'hiver en général.
De plus, elle n'est valable que si le rapport SHF reste supérieur ou égal à 0,36.

N.B. : Cette page est disponible au format pdf dans la section "Téléchargements".

⇒ Gradient de pression entre locaux